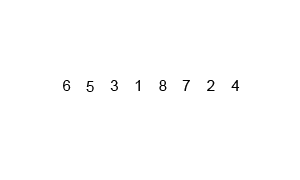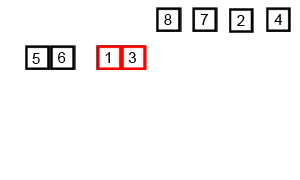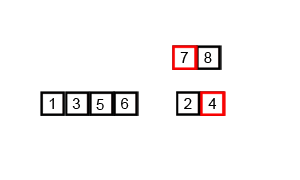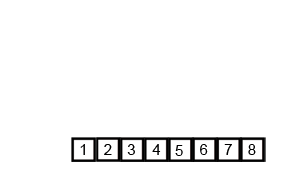Merge Sort Algorithm in Java

Merge Sort Algorithm

Merge Sort (also commonly spelled mergesort) is an efficient, general-purpose, comparison-based sorting algorithm. Most implementations produce a stable sort, which means that the implementation preserves the input order of equal elements in the sorted output. Merge sort is a divide and conquer algorithm that was invented by John von Neumann in 1945. A detailed description and analysis of bottom-up mergesort appeared in a report by Goldstine and Neumann as early as 1948. 

Merge Sort Algorithm in Data Structure example in Java programming :

public class MergeSort {

  private int[] array;
  private int[] tempMergArr;
  private int length;

  public static void main(String a[]) {

    int[] inputArr = { 32, 27, 51, 89, 1, 98, 9, 28, 65, 0 };
    MergeSort mms = new MergeSort();
    mms.sort(inputArr);

    for (int i : inputArr) {

      System.out.print(i);
      System.out.print(" ");

    }
  }

  public void sort(int inputArr[]) {
     
    this.array = inputArr;
    this.length = inputArr.length;
    this.tempMergArr = new int[length];
    doMergeSort(0, length - 1);
     
  }

  private void doMergeSort(int lowerIndex, int higherIndex) {

    if (lowerIndex < higherIndex) {
       
      int middle = lowerIndex + (higherIndex - lowerIndex) / 2;
      // Below step sorts the left side of the array
      doMergeSort(lowerIndex, middle);
      // Below step sorts the right side of the array
      doMergeSort(middle + 1, higherIndex);
      // Now merge both sides
      mergeParts(lowerIndex, middle, higherIndex);
       
    }
  }

  private void mergeParts(int lowerIndex, int middle, int higherIndex) {

    for (int i = lowerIndex; i <= higherIndex; i++) {
       
      tempMergArr[i] = array[i];
       
    }
     
    int i = lowerIndex;
    int j = middle + 1;
    int k = lowerIndex;
     
    while (i <= middle && j <= higherIndex) {
       
      if (tempMergArr[i] <= tempMergArr[j]) {
         
        array[k] = tempMergArr[i];
        i++;
         
      } else {
         
        array[k] = tempMergArr[j];
        j++;
         
      }
       
      k++;
    }
     
    while (i <= middle) {
       
      array[k] = tempMergArr[i];
      k++;
      i++;
       
    }

  }
}

OUTPUT

0 1 9 27 28 32 51 65 89 98